At Retina, we build models to predict Customer Lifetime Value (CLV). Our data science team is constantly working to refine and improve upon those models, leveraging the best academic and industry research. This article describes our results from using Recurrent Neural Networks (RNNs) to predict CLV.
Because Retina’s clients need both strategic and tactical insights into their customers, we build and test our models on both macro (cohort-level) and micro (customer-level) purchasing patterns. We use this as the basis for evaluating model performance so we can continually iterate on our models.
In this blog post, we will demonstrate how the RNN-LSTM (Recurrent Neural Network with Long / Short-term Memory) machine learning model can predict CLV nearly as accurately as other industry-leading models.
Context
To build a predictive CLV model, we start with customer transaction history. The dataset we feed into our model might look something like this:
| customer_id | order_id | order_date | order_value |
| 100022 | 100 | 2016-12-21 | 29.00 |
| 100022 | 101 | 2016-12-28 | 36.00 |
| 101046 | 200 | 2018-03-25 | 15.95 |
| … | … | … | … |
From this transaction table we can not only determine CLV, but also predict future transactions per customer—and, we can visualize this with a Timing Patterns Graph:

The above graphs shows each transaction in our transaction table as well as predicted future transactions:
- The vertical grey line marks today
- The horizontal grey lines represent individual customers
- Black dots are transactions in our transaction history
- Grey dots are transactions predicted by our model
In addition to predicting the number of transactions, our models also predict the average revenue value of each of these future transactions. When we know both the price of each future transaction and the amount of transactions there will be, we can easily compute a customer’s CLV.
Assessing a model
But how do we generate these predicted transactions and revenues? And more importantly, how do we know how accurate they are?
First, we split our transaction history data into two datasets. We do so by determining a date that falls somewhere about 80% of the way between the oldest transaction and a more recent transaction in our data set. The transactions that happened before on or before this date are part of the calibration period, and the transactions that happened after are part of the holdout period. These datasets are so named because the calibration period data is fed into the model to calibrate it, while the holdout period data is deliberately withheld to test a model’s prediction ability.
If a model can use the data provided in the calibration period to accurately predict the data in the holdout period, then we know it is a strong model.
Comparing the models
A common model used to calculate CLV is the Pareto/NBD model, though Retina currently uses the Pareto/GGG model, which is an improvement upon the Pareto/NBD model. What makes Pareto/GGG such a powerful CLV model is that it creates three gamma distributions to determine customer inter-transaction time (ITT) and churn probability. If you’d like to explore it deeper, you can read more about this model in the original paper or the BTYD package.
However, the Retina team has also developed a newer model that is being compared against Pareto/GGG today. It’s called the Long-Short-Term-Memory Recurrent Neural Network model (RNN-LSTM). This model takes in a sequence of events looks for patterns in those events leading up to the present, which allows it to predict the future. We feed the model with customer transaction history hoping it will learn future transactions in our case.
|
In the Blue Corner: Pareto/GGG |
 |
| In the Red Corner: RNN-LSTM |
Let’s see who wins this CLV Match
Results
By using our calibration/holdout technique outlined above, we were able to see the prediction strength of each of our models. We also included additional Pareto family models (BG/NBD and NBD) to provide context to our results. So, here are the results from our experiment:
| Model | Total # of Holdout Transactions | Deviations for Actual (#) | Deviation from Actual (%) | Mean Absolute Error (MAE) |
| Actual | 28,224 | n/a | n/a | 0 |
| Pareto/GGG | 28,749 | +525 | 1.9% | 1.56 |
| RNN-LSTM | 26,456 | -1,768 | 6.3% | 1.62 |
| BG/NBD | 28,733 | +509 | 1.8% | 1.70 |
| Pareto/NBD | 28,382 | +158 | 0.6% | 1.75 |
| NBD | 39,619 | 11,395 | 40% | 2.33 |
When we compare the actual number of transactions in our holdout period to the number each model predicted, we can see how well each model fared. The above table is sorted by Mean Absolute Error (MAE), or the average per customer difference between the predicted number transactions and the actual number of transactions.
With the exception of NBD, the statistical models all performed strongly (less than 10% deviation from true values) on this metric. This means they are able to successfully capture customer purchasing trends at the aggregate level. Interestingly, our RNN-LSTM model is the only model that underestimates the total number of holdout transactions.
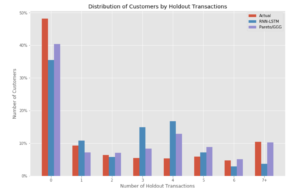
The figure compares the accuracy of both RNN-LSTM and Pareto/GGG across different purchasing amount per customer:
What this chart demonstrates is that RNN-LSTM severely underpredicts churned customers (customers who did not purchase anything in the holdout period) and over predicts 3-4 purchase customers. Pareto/GGG also underpredicts churned customers and overpredicts 3-4 purchase customers, but to a lesser degree.
Discussion
At first, Pareto/NBD appears to predict a near perfect number of transactions, this accuracy is due to the aggregate number of transactions predicted. As we seen when calculating MAE, Pareto/NBD actually performs worse on an individual level than Pareto/GGG and RNN-LSTM. CLV is a much more actionable metric at the individual level, so we decided to focus our further analysis on these two models.
Back to our CLV Boxing Match: Pareto/GGG outperforms RNN-LSTM when using MAE, but not by much. These results are exciting because it not only demonstrates the superiority of Pareto/GGG, but also the validity of RNN-LSTM as a contender for CLV calculations.
There are two concepts that become relevant beyond our results that should be discussed when considering which model is superior: extendability and explanatory power.
RNN-LSTM is a strong option for CLV calculation because it is extendable. Unlike Pareto/GGG, RNN-LSTM takes in a larger number of features that can be customized and aggregated by the data scientist running the model. This means that RNN-LSTM can be informed by site visits, emails, and even specific industry trends, to create smarter and smarter iterations.
Pareto/GGG is a strong option for CLV calculation thanks to its explanatory power. Unlike RNN-LSTM, which is essentially a black box in terms of understanding why it made a certain prediction, Pareto/GGG allows the data scientist to understand the underlying framework behind the predictions the model makes. If the model seems to underpredict churned customers, we can conclude that this is a function of an overly optimistic churn prediction gamma function. So, when the model is accurate or better than others, we can be more confident about why it is a stronger model. We are not afforded that luxury for machine learning models.
Next Steps
Finally, there are several steps that would be thrilling experiments to build off of these results. A few future iterations we are enthusiastic to try are:
- Predicting value of the transaction in the holdout instead of the number, and compare models on this metric
- Add additional relevant features to the RNN-LSTM model and see if the new architecture significantly outperforms Pareto family models
- Tune the hyperparameters of RNN-LSTM in order to see if more intelligent hyperparameter selection results in a superior model
- Modify Pareto/GGG output to produce drawn transaction sequences in order to create a direct comparison to RNN-LSTM’s forecasting capabilities
We hope this model comparison has been equally informative and entertaining, as we certainly enjoyed conducting the analysis.
Let’s connect and improve your LTV calculations!